
数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
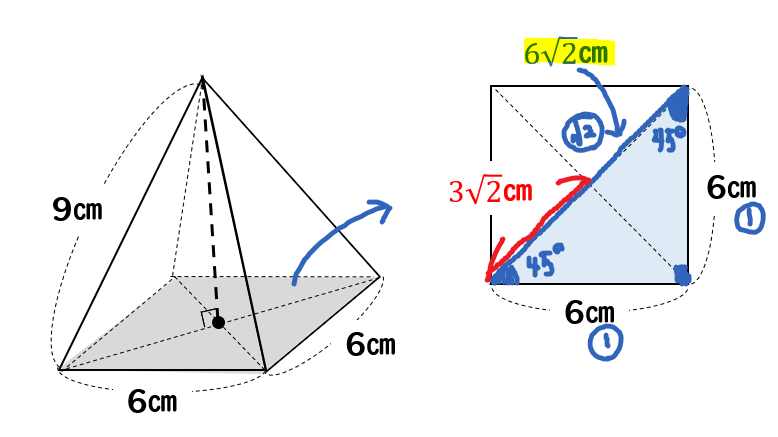
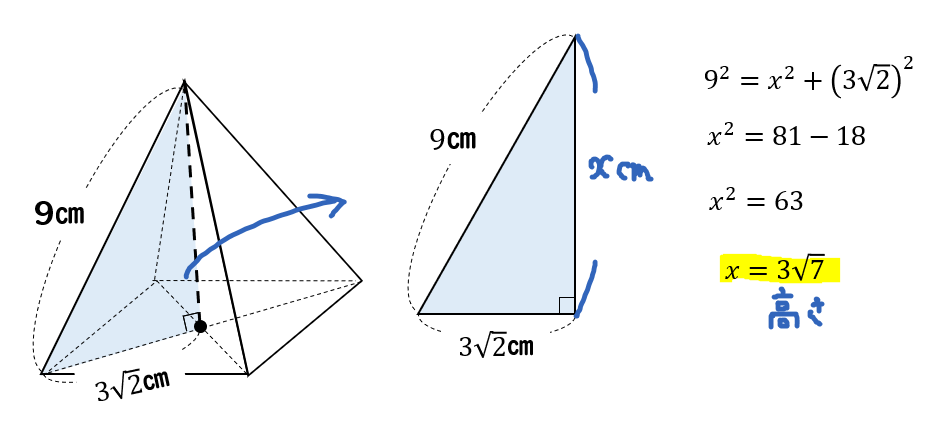
さらに、その半分の長さ まで求めておきましょう。 次に、正四角錐の高さを含む こちらの直角三角形に注目します。 すると、先ほど求めた ㎝ の辺を用いて 三平方の定理から高さを求めることが 多くの中学生が苦しむ分野である立体の「体積」と「表面積」の求め方を現役塾講師&家庭教師がわかりやすく一覧にしてまとめています。 menu メニュー 千葉県の塾を探す;
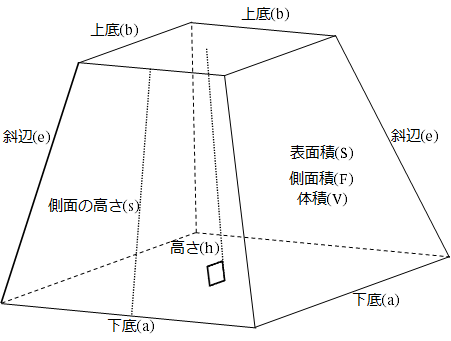
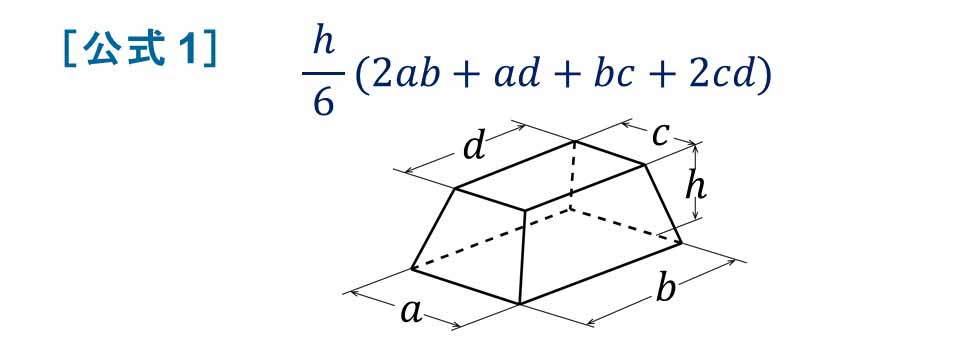
台形 体積 求め方 四辺の長さが違う
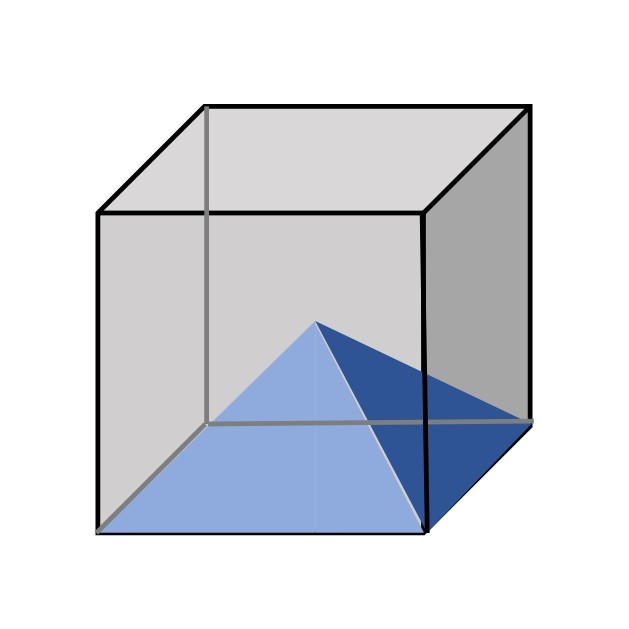
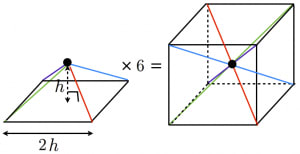
台形 体積 求め方 四辺の長さが違う-④ 四角錐の体積は? ここで、立方体の体積を思い出しましょう。 一辺がaなので、体積はa 3 でした。 さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積四角すいの体積 A: B: H: 体積: 球 球 半球 中空球 円周から体積 円柱 円
Q Tbn And9gct3xjdnufbtxwuuppawfzj1lac80hepgai6va 6s3xqejxnku6e3jsb Usqp Cau
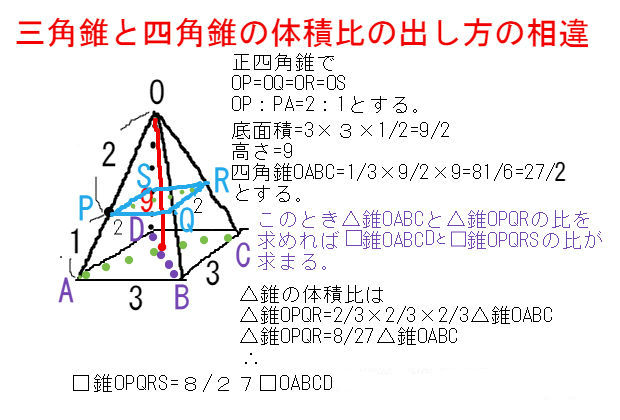
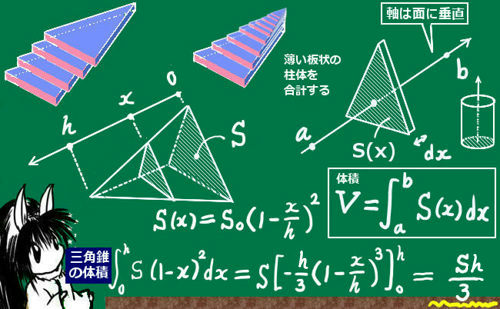
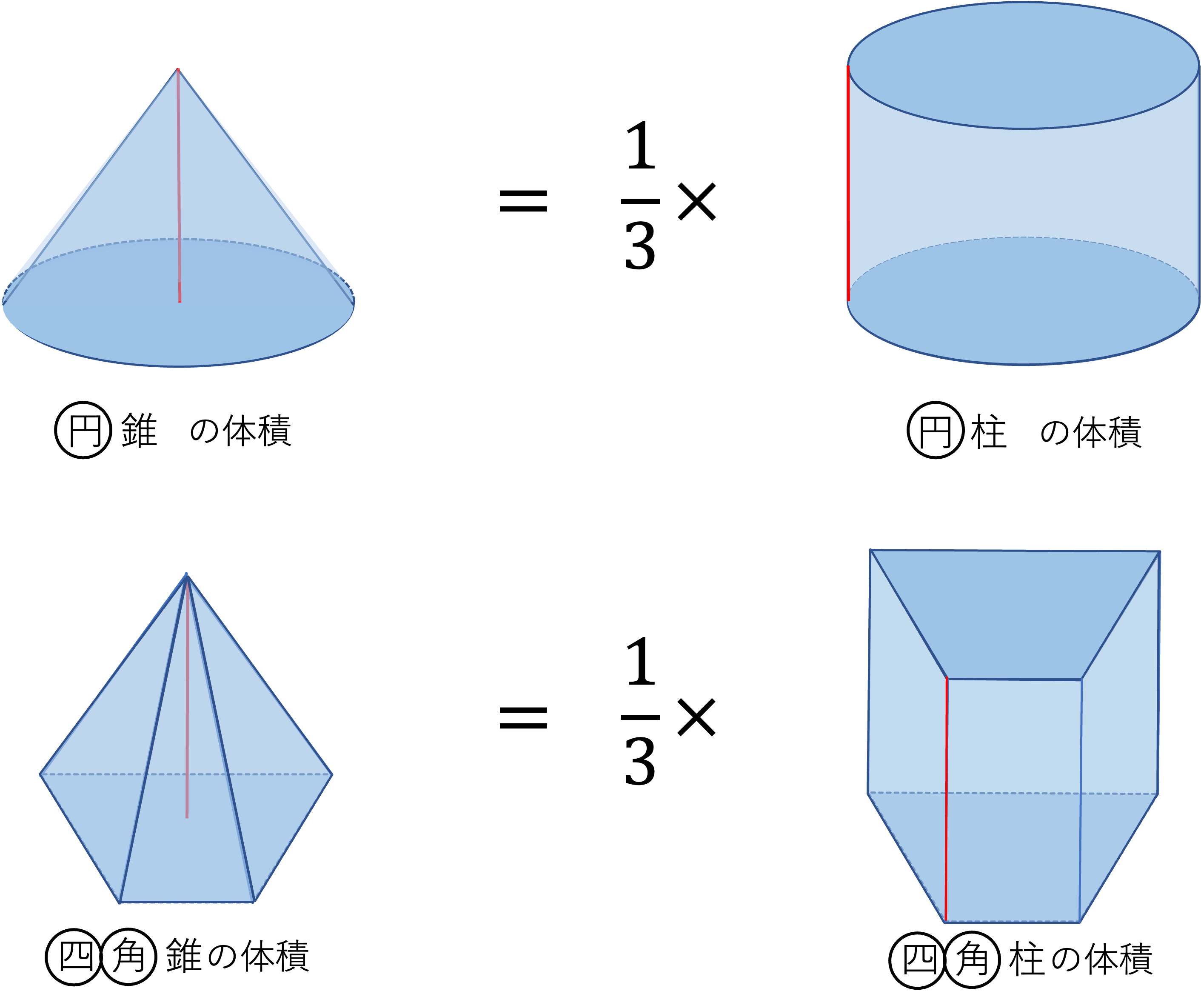
①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積を拡縮してみる ①特別な四角錐を考える 底面積が一辺 の正方形,高さが の四角錐を考え切頭ピラミッドの体積の公式 (2) の求め方はほかにも考えられますが、ピラミッドの体積の求め方 (1) さえわかれば、それほど難しいものではないよう思えます。ではエジプト人はどのようにして (1) つまり、四角錐、円錐の体積はそれぞれ (四角錐の体積) (四角柱の体積) (底面の四角形の面積) (高さ) (円錐) (円柱) (底面の円の面積) (高さ) となります。 なの
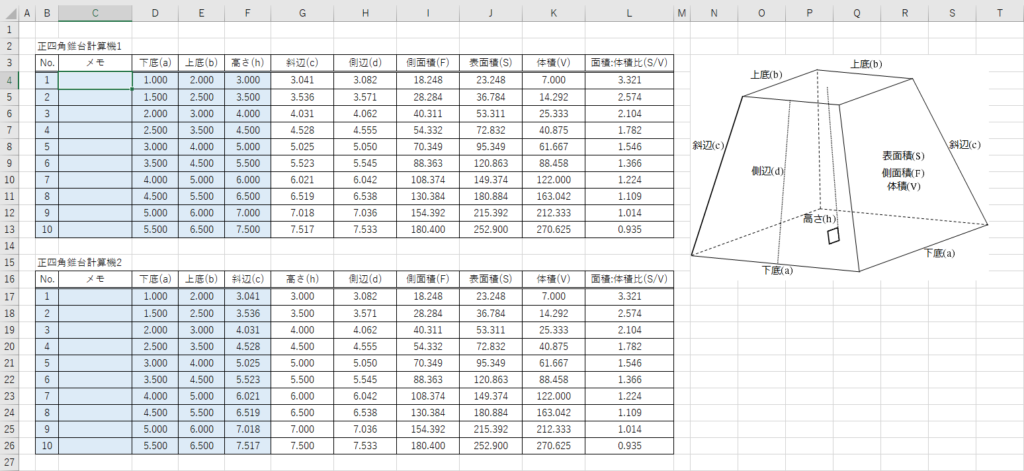
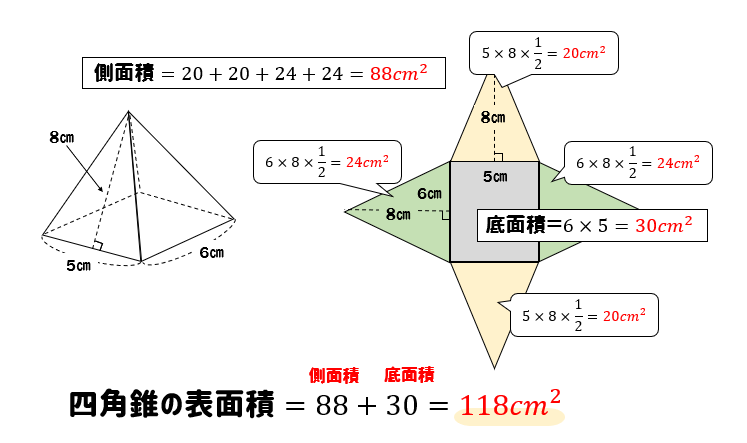
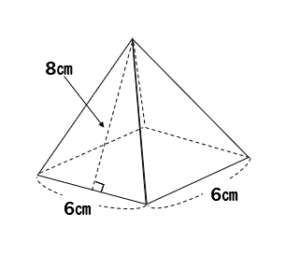
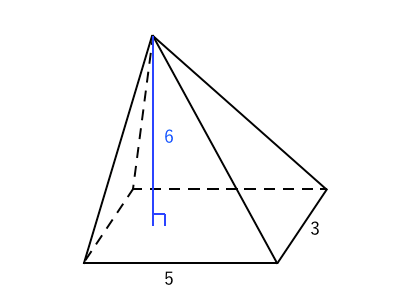
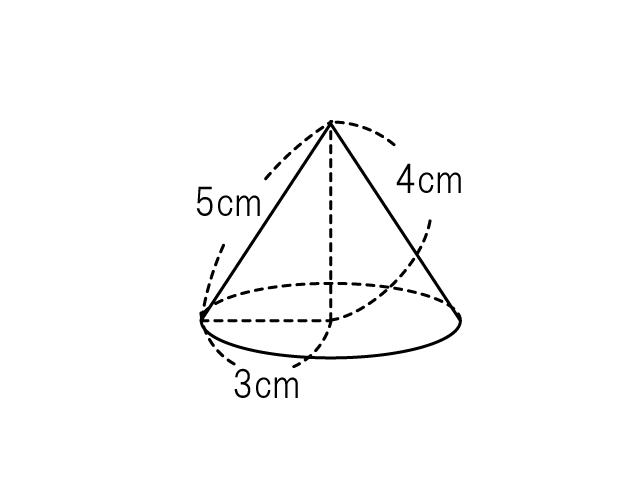
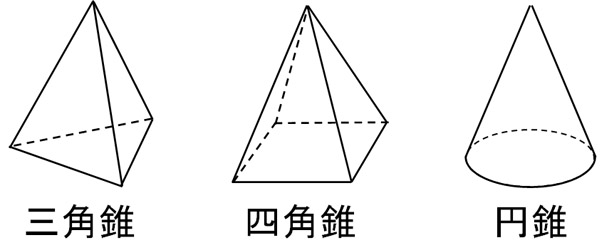
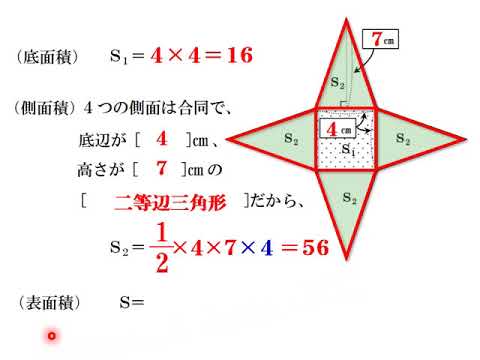
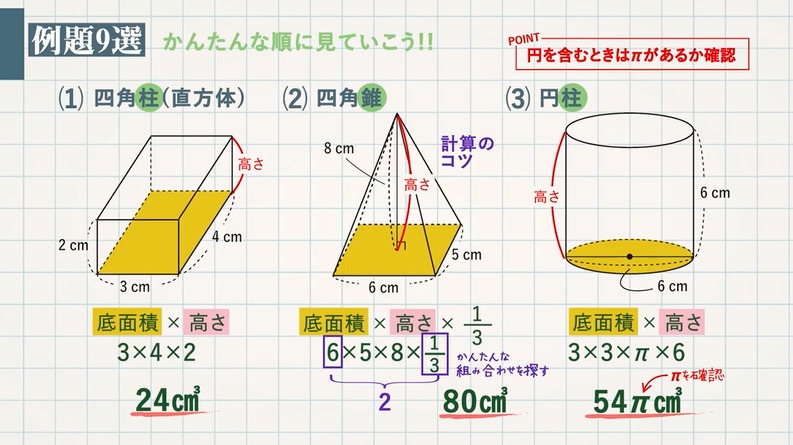
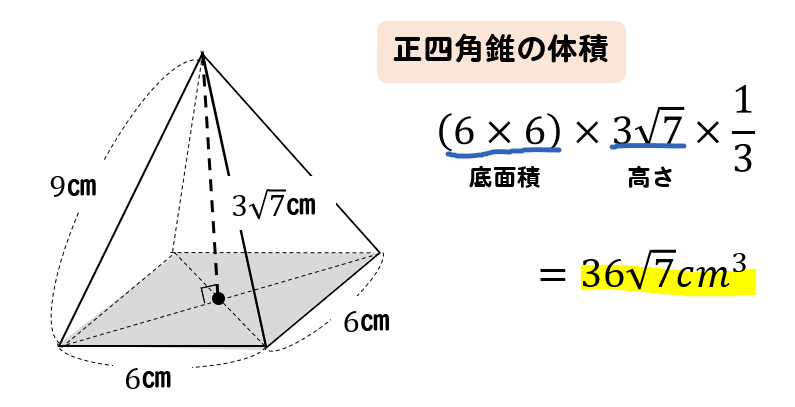
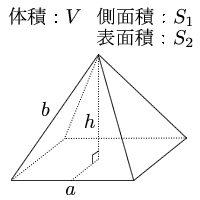
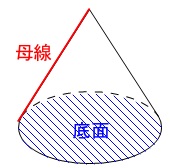
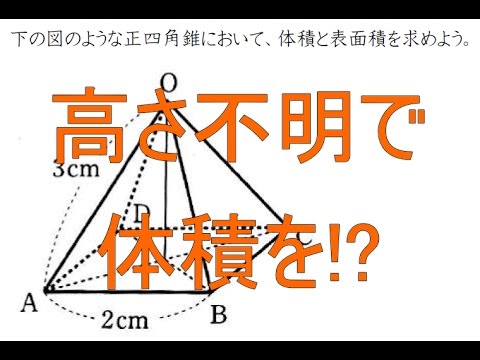
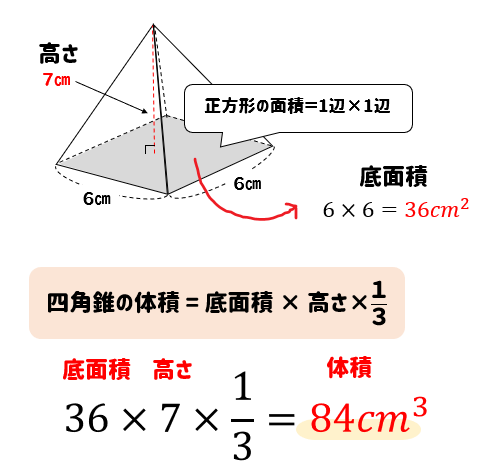
四角錐の体積の求め方 四角錐の体積は、底面積を S 、高さを h とした場合、 1/3 Sh で求められます。 四角錐の底面は、長方形や平行四辺形など、どんな四角形でも 1/3 Sh で体積を求められます。・円錐の体積の求め方 角錐や円錐の体積を出すとき、公式に当てはめるようにしましょう。最初に底面積を計算します。上図の円錐では、底面積は以下になります。 \(3×3×π=9π\) その後、公式に正四角錐の体積の求め方は次のとおり。 正四角錐の体積の求め方・\(3\)ステップ \(1\)、直角三角形の比を使って、対角線の半分の長さを求める \(2\)、三平方の定理を使って、高さを求める \(3\)
台形 体積 求め方 四辺の長さが違うのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「台形 体積 求め方 四辺の長さが違う」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |
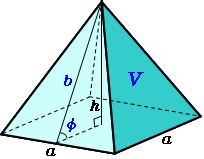
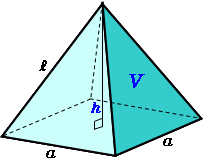
四角錐の体積の求め方・公式\(1\)ステップ 「四角錐の体積って、どうやって求めるの?」 四角錐の体積を求め方は次のとおり。 四角錐の体積の求め方 ・ 公式\(\frac{1}{3}Sh\)に底面積と高さを代入 三角錐,四角錐,円錐などの錐体の体積は 1 3 つまり,求めたい A A A の体積は V = 1 3 S B h × S S B = 1 3 S h V=\dfrac{1}{3}S_Bh\times\dfrac{S}{S_B}=\dfrac{1}{3}Sh V = 3 1 S B h ×
Incoming Term: 角錐 体積 3分の1 理由 小学生, 四角錐 高さ 求め方 中学受験, 中1 数学 円錐 表面積の求め方, 円錐 体積 3分の1 理由 小学生, 台形 体積 求め方 四辺の長さが違う,




0 件のコメント:
コメントを投稿